Mensuration is a pure formula-based topic and tricks/shortcuts are seldom applied here.
Solutions to all the mensuration problems that have appeared in CGL lately
Q. 1) 
For Prism and Calendar (figures with uniform girth) –
Lateral Surface Area = Height * Perimeter of the Base
Volume = Height * Area of the Base
In this question the Total surface area is being asked
Total Surface Area of a Prism = Lateral Surface Area + Area of the two bases
Height of the prism = 10 cm
Perimeter of the base = 5 + 12 + 13 (Calculate the hypotenuse with Pythagoras Theorem) = 30 cm
So Lateral Surface Area = 10 * 30 = 300 cm
Area of the base = 1/2 * base * height = 1/2 * 5 * 12 = 30 cm
So Total Surface Area = 300 + 2*30 = 360 cm
Answer : (A)
Q. 2)
In such questions, remember one thing SIMILARITY
r/R = h/H … (1)
where r = radius of the small cone
R = radius of Big cone
h = height of small cone
H = height of big cone
Volume of cone = 1/3 * π* r2 * h
Given, Volume of big cone = 27 * Volume of small cone
1/3 * π * R2 * H = 27 * 1/3 * π * r2 * h
27 * (r/R)^2=H/h
Put the value of r/R from equation (1)
27 * (h/H)^2 = H/h
27 * h3 = H3
Put H = 30 cm
So h = 10 cm
The question asks us the height above the base, which is (30 – h) = 30 – 10 = 20 cm
Answer : (B)
Q. 3)

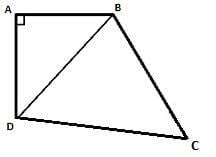
The base of the prism looks like the figure above.
AD = 12 cm, AB = 9 cm
Hence BD = 15 cm (Pythagoras Theorem)
Area of base = Area of triangle ABD + Area of triangle BDC
Area of triangle ABD = 1/2 * 9 * 12 = 54 cm
Area of triangle BDC = 84 cm (Apply Heron’s formula)
Area of base/quadrilateral = 84 + 54 = 138 cm
Volume = Height * Area of the Base
2070 = Height * 138
So, Height of the prism = 15 cm
Lateral Surface Area = Height * Perimeter of the Base
Perimeter of the base = AB + BC + CD + DA = 48 cm
Lateral Surface Area = 48 * 15 = 720 cm^2
Answer : (A)
Q. 4)

Area of the base = √3/4 * a^2, where a is the side of the equilateral triangle
Perimeter of the base = 3a
Volume of the prism = Area of the base * Height =√3/4 * a^2 * h … (1)
Lateral surface Area of the prism = Perimeter of the base * Height = 3a * h …(2)
Divide equation (1) by (2)
Volume/Area = (1/4√3) * a
40√3/120 = a/4√3 [Since Volume = 40√3 and Lateral surface Area = 120]
a = 160 * 3/120
a = 4 cm
Answer : (A)
Q. 5)

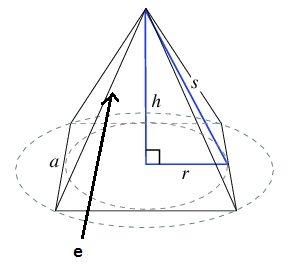
This question is about ‘Pyramid’. So let me just give you some basic understanding of Pyramids. CGL can ask questions about two types of Pyramids – Pyramid with a Triangular Base and Pyramid with a square base. Both these pyramids have different formulas. Look at the below figure and understand the labellings, i.e., Slant edge and Slant Height
In the below image, I have written formulas for both types of Pyramids. The formula for Volume is same for both the Pyramids-
V = 1/3 * A * h
where A = Area of the base (calculation of A will be different for both)
h = Height of the Pyramid
When lateral surface area is asked, you will first calculate the ‘Slant Height’. Then with the help of slant height you will find the area of one lateral face (let’s call this area M). If the pyramid is having a triangular base then multiply M with 3, to get the lateral surface area of the pyramid. And if the pyramid is having a square base, then multiply M with 4.

The area of the square is 324, hence its side is 18 cm
Volume of the pyramid = 1/3 * Area of the base * Height
1296 = 1/3 * 324 * Height
So Height = 12 cm
Slant Height of the pyramid with square base = √ (h^2 + a^2/4) = √(12^2 + 18^2/4)
Slant Height = 15cm
Area of the lateral face = 1/2 * Base * Height = 1/2 * 18 * 15 = 135 cm^2
Pyramid with a square base has 4 lateral faces, so lateral surface area of the pyramid = 4 * 135 = 540 cm^2
Answer : (D)


Leave a comment